Quantam Mechanics

[NOMS][The Care System][Family Values][Horror Movies Home][OTR][Academia][Our Existenz][Raison d etre][Action Movies][Cult Classics][War Zone][Links][Paleontology][X][Miscellaneous][Memento Mori][Sitemap]

Quantum mechanics is essential to understand the behavior of systems at atomic length scales and smaller. For example, if classical mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus, making stable atoms impossible. However, in the natural world the electrons normally remain in an unknown orbital path around the nucleus, defying classical electromagnetism.

Quantum mechanics was initially developed to provide a better explanation of the atom, especially the spectra of light emitted by different atomic species. The quantum theory of the atom was developed as an explanation for the electron's staying in its orbital, which could not be explained by Newton's laws of motion and by Maxwell's laws of classical electromagnetism.

In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function (sometimes referred to as orbitals in the case of atomic electrons), and more generally, elements of a complex vector space. This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with arbitrary accuracy. For instance, electrons may be considered to be located somewhere within a region of space, but with their exact positions being unknown. Contours of constant probability, often referred to as “clouds” may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle.

The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein exploited this idea to show that an electromagnetic wave such as light could be described by a particle called the photon with a discrete energy dependent on its frequency. This led to a theory of unity between subatomic particles and electromagnetic waves called wave–particle duality in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain “macroscopic quantum systems” such as superconductors and superfluids.

Broadly speaking, quantum mechanics incorporates four classes of phenomena that classical physics cannot account for: (I) the quantization (discretization) of certain physical quantities , (II) wave-particle duality , (III) the uncertainty principle, and (IV) quantum entanglement. Each of these phenomena is described in detail in subsequent sections.

The history of quantum mechanics^[2] began essentially with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy is radiated and absorbed in quantities divisible by discrete ‘energy elements’, E, such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula

where h is Planck's Action Constant . Although Planck insisted^[3] that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself, in 1905, to explain the photoelectric effect (1839), i.e. that shining light on certain materials can function to eject electrons from the material, Albert Einstein^[4] postulated, as based on Planck’s quantum hypothesis, that light itself consists of individual quanta, which later came to be called photons (1926). From Einstein's simple postulation was borne a flurry of debating, theorizing and testing, and thus, the entire field of quantum physics.

The modern world of physics is founded on the to tested and demonstrably sound theories of general relativity and quantum mechanics —theories which appear to contradict one another. The defining postulates of both Einstein's theory of relativity and quantum theory are indisputably supported by rigorous and repeated empirical evidence. However, while they do not directly contradict each other theoretically (at least with regard to primary claims), they are resistant to being incorporated within one cohesive model.

Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly inventive in this field, he did not accept the more philosophical consequences and interpretations of quantum mechanics, such as the lack of deterministic causality and the assertion that a single subatomic particle can occupy numerous areas of space at one time. He also was the first to notice some of the apparently exotic consequences of entanglement and used them to formulate the Einstein-Podolsky-Rosen paradox , in the hope of showing that quantum mechanics had unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see Bell inequality ) that Einstein's assumption was correct, but had to be completed by hidden variables and thus based on wrong philosophical assumptions. According to the paper of J. Bell and the Copenhagen interpretation (the common interpretation of quantum mechanics by physicists for decades), and contrary to Einstein's ideas, quantum mechanics was

neither a "realistic" theory (since quantum measurements do not state pre-existing properties, but rather they prepare properties)

nor a local theory (essentially not, because the state vector $\scriptstyle |\psi\rangle$ determines simultaneously the probability amplitudes at all sites, $|\psi\rangle\to\psi(\mathbf r), \forall \mathbf r$ ).

The Einstein-Podolsky-Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner, although the two particles can be an arbitrary distance apart; however, this effect does not violate causality, since no transfer of information happens. These experiments are the basis of some of the most topical applications of the theory, quantum cryptography, which works well, although at small distances of typically $\scriptstyle \le$ 1000 km, being on the market since 2004.

There do exist quantum theories which incorporate special relativity—for example, quantum electrodynamics (QED), which is currently the most accurately tested physical theory ^[5]—and these lie at the very heart of modern particle physics. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those applications. However, the lack of a correct theory of quantum gravity is an important issue in cosmology.

Inconsistencies arise when one tries to join the quantum laws with general relativity, a more elaborate description of spacetime which incorporates gravitation. Resolving these inconsistencies has been a major goal of twentieth- and twenty-first-century physics. Many prominent physicists, including Stephen Hawking, have labored in the attempt to discover a "Grand Unification Theory " that combines not only different models of subatomic physics, but also derives the universe's four forces—the strong force, electromagnetism, weak force, and gravity — from a single force or phenomenon.

Predictions of quantum mechanics have been verified experimentally to a very high degree of accuracy. Thus, the current logic of correspondence principle between classical and quantum mechanics is that all objects obey laws of quantum mechanics, and classical mechanics is just a quantum mechanics of large systems (or a statistical quantum mechanics of a large collection of particles). Laws of classical mechanics thus follow from laws of quantum mechanics at the limit of large systems or large quantum numbers.

Main differences between classical and quantum theories have already been mentioned above in the remarks on the Einstein-Podolsky-Rosen paradox. Essentially the difference boils down to the statement that quantum mechanics is coherent (addition of amplitudes), whereas classical theories are incoherent (addition of intensities). Thus, such quantities as coherence lengths and coherence times come into play. For microscopic bodies the extension of the system is certainly much smaller than the coherence length; for macroscopic bodies one expects that it should be the other way round.

This is in accordance with the following observations:

Many “macroscopic” properties of “classic” systems are direct consequences of quantum behavior of its parts. For example, stability of bulk matter (which consists of atoms and molecules which would quickly collapse under electric forces alone), rigidity of this matter, mechanical, thermal, chemical, optical and magnetic properties of this matter—they are all results of interaction of electric charges under the rules of quantum mechanics.

While the seemingly exotic behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with extremely fast-moving or extremely tiny particles, the laws of classical “Newtonian” physics still remain accurate in predicting the behavior of surrounding (“large”) objects—of the order of the size of large molecules and bigger—at velocities much smaller than the velocity of light.

There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the transformation theory proposed by Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics, matrix mechanics (invented by Werner Heisenberg)^[6] and wave mechanics (invented by Erwin Schrödinger).

In this formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).

Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions about probability distributions; that is, the probability of obtaining each of the possible outcomes from measuring an observable. Oftentimes these results are skewed by many causes, such as dense probability clouds or quantum state nuclear attraction. Much of the time, these small anomalies are attributed to different causes such as quantum dislocation. Naturally, these probabilities will depend on the quantum state at the instant of the measurement. When the probability amplitudes of four or more quantum nodes are similar, it is called a quantum parallelism . There are, however, certain states that are associated with a definite value of a particular observable. These are known as "eigenstates" of the observable ("eigen" can be roughly translated from German as inherent or as a characteristic). In the everyday world, it is natural and intuitive to think of everything being in an eigenstate of every observable. Everything appears to have a definite position, a definite momentum, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values for the position or momentum of a certain particle in a given space in a finite time; rather, it only provides a range of probabilities of where that particle might be. Therefore, it became necessary to use different words for (a) the state of something having an uncertainty relation and (b) a state that has a definite value. The latter is called the "eigenstate" of the property being measured.

For example, consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as a wave. Therefore, its quantum state can be represented as a wave, of arbitrary shape and extending over all of space, called a wave function. The position and momentum of the particle are observables. The Uncertainty Principle of quantum mechanics states that both the position and the momentum cannot simultaneously be known with infinite precision at the same time. However, one can measure just the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large at a particular position x, and almost zero everywhere else. If one performs a position measurement on such a wavefunction, the result x will be obtained with almost 100% probability. In other words, the position of the free particle will almost be known. This is called an eigenstate of position (mathematically more precise: a generalized eigenstate (eigendistribution) ). If the particle is in an eigenstate of position then its momentum is completely unknown. An eigenstate of momentum, on the other hand, has the form of a plane wave. It can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate . If the particle is in an eigenstate of momentum then its position is completely blurred out.

Usually, a system will not be in an eigenstate of whatever observable we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or generalized eigenstate) of that observable. This process is known as wavefunction collapse . It involves expanding the system under study to include the measurement device, so that a detailed quantum calculation would no longer be feasible and a classical description must be used. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x₀, neither an eigenstate of position nor of momentum. When one measures the position of the particle, it is impossible to predict with certainty the result that we will obtain. It is probable, but not certain, that it will be near x₀, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.

Wave functions can change as time progresses. An equation known as the Schrödinger equation describes how wave functions change in time, a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.

Some wave functions produce probability distributions that are constant in time. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus (Fig. 1). (Note that only the lowest angular momentum states, labeled s, are spherically symmetric).

The time evolution of wave functions is deterministic in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time. During a measurement , the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., random .

The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates , in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Interpretations of quantum mechanics have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the relative state interpretation . The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled , so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.

In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac^[7] and John von Neumann^[8], the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors") residing in a complex separable Hilbert space (variously called the "state space" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally-Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.

The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.

The inner product between two state vectors is a complex number known as a probability amplitude. During a measurement, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator - which explains the choice of Hermitian operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.

The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the wave-like behavior of quantum states.

It turns out that analytic solutions of Schrödinger's equation are only available for a small number of model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen molecular ion and the hydrogen atom are the most important representatives. Even the helium atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as perturbation theory one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak potential energy. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of quantum chaos.

An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of action principles in classical mechanics.

The fundamental rules of quantum mechanics are very broad. They assert that the state space of a system is a Hilbert space and the observables are Hermitian operators acting on that space, but do not tell us which Hilbert space or which operators, or if it even exists. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers. In other words, classic mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the classical or correspondence limit. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit.

When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.

Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction.

The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical 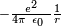$\scriptstyle -\frac{e^2}{4 \pi\ \epsilon_0\ } \frac{1}{r}$ Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.

Quantum field theories for the strong nuclear force and the weak nuclear force have been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of the subnuclear particles: quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory known as electroweak theory , by the physicists Abdus Salam, Sheldon Glashow and Steven Weinberg.

It has proven difficult to construct quantum models of gravity , the remaining fundamental force . Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity, the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as string theory are among the possible candidates for a future theory of quantum gravity restricts the acceptable solutions of the wavefunction. At each wall:

EXISTENZ HOME