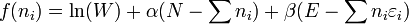Fermi–Dirac and Bose–Einstein statistics apply when quantum effects are important and the particles are "indistinguishable". Quantum effects appear if the concentration of particles (N/V) ≥ nq. Here nq is the quantum concentration, for which the interparticle distance is equal to the thermal de Broglie wavelength, so that the wavefunctions of the particles are touching but not overlapping. Fermi–Dirac statistics apply to fermions (particles that obey the Pauli exclusion principle), and Bose–Einstein statistics apply to bosons. As the quantum concentration depends on temperature; most systems at high temperatures obey the classical (Maxwell–Boltzmann) limit unless they have a very high density, as for a white dwarf. Both Fermi–Dirac and Bose–Einstein become Maxwell–Boltzmann statistics at high temperature or at low concentration.
The expected number of particles in an energy state i for B–E statistics is:
- ni is the number of particles in state i
- gi is the degeneracy of state i
- εi is the energy of the ith state
- μ is the chemical potential
- k is Boltzmann's constant
- T is absolute temperature
- gi is the degeneracy of state i
History
In the early 1920s Satyendra Nath Bose, a professor of University of Dhaka in British India was intrigued by Einstein's theory of light waves being made of particles called photons. Bose was interested in deriving Planck's radiation formula, which Planck obtained largely by guessing. In 1900 Max Planck had derived his formula by manipulating the math to fit the empirical evidence. Using the particle picture of Einstein, Bose was able to derive the radiation formula by systematically developing a statistics of massless particles without the constraint of particle number conservation. Bose derived Planck's Law of Radiation by proposing different states for the photon. Instead of statistical independence of particles, Bose put particles into cells and described statistical independence of cells of phase space. Such systems allow two polarization states, and exhibit totally symmetric wavefunctions.
A derivation of the Bose–Einstein distribution
Let  be the number of ways of distributing
be the number of ways of distributing  particles among the
particles among the 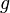 sublevels of an energy level. There is only one way of distributing
sublevels of an energy level. There is only one way of distributing  particles with one sublevel, therefore
particles with one sublevel, therefore  .
It is easy to see that there are
.
It is easy to see that there are  ways of distributing
ways of distributing  particles in two sublevels which we will write as:
particles in two sublevels which we will write as:
where we have used the following theorem involving binomial coefficients:
Continuing this process, we can see that  is just a binomial coefficient (See Notes below)
is just a binomial coefficient (See Notes below)
Using the 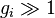 approximation and using Stirling's approximation for the
factorials
approximation and using Stirling's approximation for the
factorials  gives
gives
It can be shown thermodynamically that  ,
where
,
where  is Boltzmann's constant and
is Boltzmann's constant and  is the temperature.
is the temperature.
It can also be shown that  ,
where
,
where  is the chemical
potential, so that finally:
is the chemical
potential, so that finally:
Note that the above formula is sometimes written:
where  is the absolute activity.
is the absolute activity.
![]() Copyright(c) 2007
- 2012. All rights reserved.
Copyright(c) 2007
- 2012. All rights reserved.

 and where:
and where: and to Rayleigh-Jeans distribution for
and to Rayleigh-Jeans distribution for  ,
namely
,
namely  .
. ,
each level having energy
,
each level having energy  and containing a total of
and containing a total of  particles. Suppose each level contains
particles. Suppose each level contains  distinct sublevels, all of which have the same energy, and which are
distinguishable. For example, two particles may have different momenta, in which
case they are distinguishable from each other, yet they can still have the same
energy. The value of
distinct sublevels, all of which have the same energy, and which are
distinguishable. For example, two particles may have different momenta, in which
case they are distinguishable from each other, yet they can still have the same
energy. The value of 
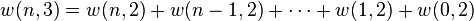
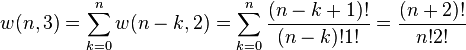



 is maximised, subject to the constraint that there be a fixed number of
particles, and a fixed energy. The maxima of
is maximised, subject to the constraint that there be a fixed number of
particles, and a fixed energy. The maxima of  occur at the value of
occur at the value of  and, since it is easier to accomplish mathematically, we will maximise the
latter function instead. We constrain our solution using Lagrange
multipliers forming the function:
and, since it is easier to accomplish mathematically, we will maximise the
latter function instead. We constrain our solution using Lagrange
multipliers forming the function: