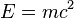In physics, mass–energy equivalence is the concept that the mass of a body is a measure of its energy content. In this concept the total internal energy E of a body at rest is equal to the product of its rest mass m and a suitable conversion factor to transform from units of mass to units of energy. If the body is not stationary relative to the observer then account must be made for relativistic effects where m is given by the relativistic mass and E the relativistic energy of the body. Albert Einstein proposed mass–energy equivalence in 1905 in one of his Annus Mirabilis papers entitled "Does the inertia of a body depend upon its energy-content?" The equivalence is described by the famous equation

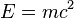
where E is energy, m is mass, and c is the speed of light in a vacuum. The formula is dimensionally consistent and does not depend on any specific system of measurement units. For example, in many systems of natural units, the speed of light is set equal to 1, and the formula becomes the identity E = m; hence the term mass–energy equivalence.

The equation E = mc² indicates that energy always exhibits mass in whatever form the energy takes. Mass–energy equivalence also means that mass conservation becomes a restatement, or requirement, of the law of energy conservation, which is the first law of thermodynamics. Mass–energy equivalence does not imply that mass may be “converted” to energy, and indeed implies the opposite. Modern theory holds that neither mass nor energy may be destroyed, but only moved from one location to another.

In physics, mass must be differentiated from matter, a more poorly-defined idea in the physical sciences. Matter, when seen as certain types of particles, can be created and destroyed, but the precursors and products of such reactions retain both the original mass and energy, both of which remain unchanged (conserved) throughout the process. Letting the m in E = mc² stand for a quantity of "matter" may lead to incorrect results, depending on which of several varying definitions of "matter" are chosen.

E = mc² has sometimes been used as an explanation for the origin of energy in nuclear processes, but mass–energy equivalence does not explain the origin of such energies. Instead, this relationship merely indicates that the large amounts of energy released in such reactions may exhibit enough mass that the mass-loss may be measured, when the released energy (and its mass) have been removed from the system.

Einstein was not the first to propose a mass–energy relationship (see History). However, Einstein was the first scientist to propose the E = mc² formula and the first to interpret mass–energy equivalence as a fundamental principle that follows from the relativistic symmetries of space and time.

Mass–energy equivalence states that any object has a certain energy, even when it is stationary. In Newtonian mechanics, a motionless body has no kinetic energy, and it may or may not have other amounts of internal stored energy, like chemical energy or thermal energy, in addition to any potential energy it may have from its position in a field of force. In Newtonian mechanics, all of these energies are much smaller than the mass of the object times the speed of light squared.

In relativity, all of the energy that moves along with an object adds up to the total mass of the body, which measures how much it resists deflection. Each potential and kinetic energy makes a proportional contribution to the mass. Even a single photon traveling in empty space has a relativistic mass, which is its energy divided by c². If a box of ideal mirrors contains light, the mass of the box is increased by the energy of the light, since the total energy of the box is its mass.

In relativity, removing energy is removing mass, and for an observer in the center of mass frame, the formula m = E/c² indicates how much mass is lost when energy is removed. In a chemical or nuclear reaction, the mass of the atoms that come out is less than the mass of the atoms that go in, and the difference in mass shows up as heat and light which has the same relativistic mass as the difference (and also the same invariant mass in the center of mass frame of the system). In this case, the E in the formula is the energy released and removed, and the mass m is how much the mass decreases. In the same way, when any sort of energy is added to an isolated system, the increase in the mass is equal to the added energy divided by c². For example, when water is heated in a microwave oven, the oven adds about 1.11×10⁻¹⁷ kg of mass for every joule of heat added to the water.

An object moves with different speed in different frames, depending on the motion of the observer, so the kinetic energy in both Newtonian mechanics and relativity is frame dependent. This means that the amount of relativistic energy, and therefore the amount of relativistic mass, that an object is measured to have depends on the observer. The rest mass is defined as the mass that an object has when it isn't moving (or when an inertial frame is chosen such that it is not moving). The term also applies to the invariant mass of systems when the system as a whole isn't "moving" (has no net momentum). The rest and invariant masses are the smallest possible value of the mass of the object or system. They also are conserved quantities, so long as the system is closed. Because of the way they are calculated, the effects of moving observers are subtracted, so these quantities do not change with the motion of the observer.

The rest mass is almost never additive: the rest mass of an object is not the sum of the rest masses of its parts. The rest mass of an object is the total energy of all the parts, including kinetic energy, as measured by an observer that sees the center of the mass of the object to be standing still. The rest mass adds up only if the parts are standing still and don't attract or repel, so that they don't have any extra kinetic or potential energy. The other possibility is that they have a positive kinetic energy and a negative potential energy that exactly cancels.

The difference between the rest mass of a bound system and of the unbound parts is exactly proportional to the binding energy of the system. A water molecule weighs a little less than two free hydrogen atoms and an oxygen atom; the minuscule mass difference is the energy that is needed to split the molecule into three individual atoms (divided by c²), and which was given off as heat when the molecule formed (this heat had mass). Likewise, a stick of dynamite weighs a little bit more than the fragments after the explosion, so long as the fragments are cooled and the heat removed; the mass difference is the energy/heat that is released when the dynamite explodes (when it escapes, the mass associated with it escapes, but total mass is conserved). The change in mass only happens when the system is open, and the energy escapes. If a stick of dynamite is blown up in a hermetically sealed chamber, the mass of the chamber and fragments, the heat, sound, and light would still be equal to the original mass of the chamber and dynamite. This would in theory also happen, even with a nuclear bomb, if it could be kept in a chamber which did not rupture.

Massless particles

In relativity, all energy moving along with a body adds up to the total energy, which is exactly proportional to the relativistic mass. Even a single photon, graviton, or neutrino traveling in empty space has a relativistic mass, which is its energy divided by c². But the rest mass of a photon is slightly subtler to define in terms of physical measurements, because a photon is always moving at the speed of light—it is never at rest.

If you run away from a photon in the direction it travels, having it chase you, when the photon catches up to you the photon will be seen as having less energy. The faster you were traveling when it catches you, the less energy it will have. As you approach the speed of light, the photon looks redder and redder, by Doppler shift (the Doppler shift is the relativistic formula), and the energy of a very long-wavelength photon approaches zero. This is why a photon is massless; this means that the rest mass of a photon is zero.

Two photons moving in different directions can't both be made to have arbitrarily small total energy by changing frames, or by chasing them. The reason is that in a two-photon system, the energy of one photon is decreased by chasing it, but the energy of the other will increase. Two photons not moving in the same direction have an inertial frame where the combined energy is smallest, but not zero. This is called the center of mass frame or the center of momentum frame; these terms are almost synonyms (the center of mass frame is the special case of a center of momentum frame where the center of mass is put at the origin). The most that chasing a pair of photons can accomplish to decrease their energy is to put the observer in frame where the photons have equal energy and are moving directly away from each other. In this frame, the observer is now moving in the same direction and speed as the center of mass of the two photons. The total momentum of the photons is now zero, since their momentums are equal and opposite. In this frame the two photons, as a system, have a mass equal to their total energy divided by c². This mass is called the invariant mass of the pair of photons together. It is the smallest mass and energy the system may be seen to have, by any observer. It is only the invariant mass of a two-photon system that can be used to make a single particle with the same rest mass.

If the photons are formed by the collision of a particle and an antiparticle, the invariant mass is the same as the total energy of the particle and antiparticle (their rest energy plus the kinetic energy), in the center of mass frame, where they will automatically be moving in equal and opposite directions (since they have equal momentum in this frame). If the photons are formed by the disintegration of a single particle with a well-defined rest mass, like the neutral pion, the invariant mass of the photons is equal to rest mass of the pion. In this case, the center of mass frame for the pion is just the frame where the pion is at rest, and the center of mass doesn't change after it disintegrates into two photons. After the two photons are formed, their center of mass is still moving the same way the pion did, and their total energy in this frame adds up to the mass energy of the pion. Thus, by calculating the invariant mass of pairs of photons in a particle detector, pairs can be identified that were probably produced by pion disintegration.

Max Planck pointed out that the mass–energy equivalence formula implied that bound systems would have a mass less than the sum of their constituents, once the binding energy had been allowed to escape. However, Planck was thinking about chemical reactions, where the binding energy is too small to measure. Einstein suggested that radioactive materials such as radium would provide a test of the theory, but even though a large amount of energy is released per atom in radium, due to the half-life of the substance (1602 years), only a small fraction of radium atoms decay over experimentally measureable period of time.

Once the nucleus was discovered, experimenters realized that the very high binding energies of the atomic nuclei should allow calculation of their binding energies, simply from mass differences. But it was not until the discovery of the neutron in 1932, and the measurement of the neutron mass, that this calculation could actually be performed (see nuclear binding energy for example calculation). A little while later, the first transmutation reactions (such as ⁷Li + p → 2 ⁴He) verified Einstein's formula to an accuracy of ±0.5%.

The mass–energy equivalence formula was used in the development of the atomic bomb. By measuring the mass of different atomic nuclei and subtracting from that number the total mass of the protons and neutrons as they would weigh separately, one gets the exact binding energy available in an atomic nucleus. This is used to calculate the energy released in any nuclear reaction, as the difference in the total mass of the nuclei that enter and exit the reaction.

Copyright(c) 2007 - 2012. All rights reserved.

RAISON D'ETRE