The Einstein field equations (EFE) or Einstein's equations are a set of ten equations in Albert Einstein's theory of general relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy. First published by Einstein in 1915 as a tensor equation, the EFE equate spacetime curvature (expressed by the Einstein tensor) with the energy and momentum within that spacetime (expressed by the stress-energy tensor).
Similar to the way that electromagnetic fields are determined using charges and currents via Maxwell's equations, the EFE are used to determine the spacetime geometry resulting from the presence of mass-energy and linear momentum, that is, they determine the metric tensor of spacetime for a given arrangement of stress-energy in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of non-linear partial differential equations when used in this way. The solutions of the EFE are the components of the metric tensor. The inertial trajectories of particles and radiation (geodesics) in the resulting geometry are then calculated using the geodesic equation.
As well as obeying local energy-momentum conservation, the EFE reduce to Newton's law of gravitation where the gravitational field is weak.
Solution techniques for the EFE include simplifying assumptions such as symmetry. Special classes of exact solutions are most often studied as they model many gravitational phenomena, such as rotating black holes and the expanding universe. Further simplification is achieved in approximating the actual spacetime as flat spacetime with a small deviation, leading to the linearised EFE. These equations are used to study phenomena such as gravitational waves.
Mathematical form
The Einstein field equations (EFE) may be written in the form:
where  is the Ricci curvature tensor,
is the Ricci curvature tensor, 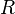 the scalar
curvature,
the scalar
curvature, 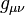 the metric tensor,
the metric tensor, 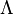 is the cosmological constant,
is the cosmological constant, 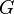 is Newton's gravitational constant,
is Newton's gravitational constant,  the speed of light,
and
the speed of light,
and  the stress-energy tensor.
the stress-energy tensor.
The EFE is a tensor equation relating a set of symmetric 4 x 4 tensors. It is written here using the abstract index notation. Each tensor has 10 independent components. Given the freedom of choice of the four spacetime coordinates, the independent equations reduce to 6 in number.
Although the Einstein field equations were initially formulated in the context of a four-dimensional theory, some theorists have explored their consequences in n dimensions. The equations in contexts outside of general relativity are still referred to as the Einstein field equations. The vacuum field equations define Einstein manifolds.
Despite the simple appearance of the equations they are, in fact, quite complicated. Given a specified distribution of matter and energy in the form of a stress-energy tensor, the EFE are understood to be equations for the metric tensor gμν, as both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE are a system of 10 coupled, nonlinear, hyperbolic-elliptic partial differential equations.
One can write the EFE in a more compact form by defining the Einstein tensor
where the cosmological term has been absorbed into the stress-energy tensor as dark energy.
Using geometrized units where G = c = 1, this can be rewritten as
These equations, together with the geodesic equation, form the core of the mathematical formulation of general relativity.
Sign convention
The above form of the EFE is the standard established by Misner, Thorne, and Wheeler. The authors analyzed all conventions that exist and classified according to the following three signs (S1, S2, S3):
The third sign above is related to the choice of convention for the Ricci tensor:
With these definitions Misner, Thorne, and Wheeler classify
themselves as 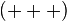 ,
whereas Weinberg (1972) is
,
whereas Weinberg (1972) is  ,
Peebles (1980) and Efstathiou (1990) are
,
Peebles (1980) and Efstathiou (1990) are  while Peacock (1994), Rindler (1977), Atwater (1974), Collins Martin &
Squires (1989) are
while Peacock (1994), Rindler (1977), Atwater (1974), Collins Martin &
Squires (1989) are  .
.
The sign of the (very small) cosmological term would change in both these versions, if the +--- metric sign convention is used rather than the MTW −+++ metric sign convention adopted here.
Equivalent formulations
Einstein's field equations can be rewritten in the following equivalent "trace-reversed" form
which may be more convenient in some cases (for example, when one is interested in weak-field limit and can replace gμν in the expression on the right with the Minkowski tensor without significant loss of accuracy).
The cosmological constant
Einstein modified his original field equations to include a cosmological term proportional to the metric
The constant Λ is the cosmological constant. Since Λ is constant, the energy conservation law is unaffected.
The cosmological constant term was originally introduced by Einstein to allow for a static universe (i.e., one that is not expanding or contracting). This effort was unsuccessful for two reasons: the static universe described by this theory was unstable, and observations of distant galaxies by Hubble a decade later confirmed that our universe is, in fact, not static but expanding. So Λ was abandoned, with Einstein calling it the "biggest blunder [he] ever made". For many years the cosmological constant was almost universally considered to be 0.
Despite Einstein's misguided motivation for introducing the cosmological constant term, there is nothing inconsistent with the presence of such a term in the equations. Indeed, recent improved astronomical techniques have found that a positive value of Λ is needed to explain some observations.
The vacuum energy is constant and given by
Conservation of energy and momentum
General relativity is consistent with the local conservation of energy and momentum expressed as
which expresses the local conservation of stress-energy. This conservation law is a physical requirement. With his field equations Einstein ensured that general relativity is consistent with this conservation condition.
Nonlinearity
The nonlinearity of the EFE distinguishes general relativity from many other fundamental physical theories. For example, Maxwell's equations of electromagnetism are linear in the electric and magnetic fields, and charge and current distributions (i.e. the sum of two solutions is also a solution); another example is Schrödinger's equation of quantum mechanics which is linear in the wavefunction.
The correspondence principle
The EFE reduce to Newton's law of gravity by using both the weak-field approximation and the slow-motion approximation. In fact, the constant appearing in the EFE is determined by making these two approximations.
If the energy-momentum tensor Tμν is zero in the region under consideration, then the field equations are also referred to as the vacuum field equations. By setting Tμν = 0 in the full field equations, the vacuum equations can be written as
Taking the trace of this (contracting with gμν) and using the fact that gμνgμν = 4, we get
Substituting back, we get an equivalent form of the vacuum field equations
In the case of nonzero cosmological constant, the equations are
The solutions to the vacuum field equations are called vacuum solutions. Flat Minkowski space is the simplest example of a vacuum solution. Nontrivial examples include the Schwarzschild solution and the Kerr solution.
Manifolds with a vanishing Ricci tensor, Rμν = 0, are referred to as Ricci-flat manifolds and manifolds with a Ricci tensor proportional to the metric as Einstein manifolds.
Einstein–Maxwell equations
If the energy-momentum tensor Tμν is that of an electromagnetic field in free space, i.e. if the electromagnetic stress-energy tensor
is used, then the Einstein field equations are called the Einstein–Maxwell equations (with cosmological constant Λ, taken to be zero in conventional relativity theory):
Additionally, the covariant Maxwell Equations are also applicable in free space:
where the semicolon represents a covariant derivative, and the brackets denote anti-symmetrization. The first equation asserts that the 4-divergence of the two-form F is zero, and the second that its exterior derivative is zero. From the latter, it follows by the Poincaré lemma that in a coordinate chart it is possible to introduce an electromagnetic field potential Aα such that
![]() Copyright(c) 2007
- 2012. All rights reserved.
Copyright(c) 2007
- 2012. All rights reserved.
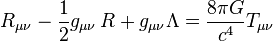



![g_{\mu \nu}~~=[S1] \times \operatorname{diag}(-1,+1,+1,+1)](http://upload.wikimedia.org/math/a/c/9/ac9fa8b1a249ac1a5f78da8f6bc365d7.png)
![{R^\mu}_{a \beta \gamma}=[S2] \times (\Gamma^\mu_{a \gamma,\beta}-\Gamma^\mu_{a \beta,\gamma}+\Gamma^\mu_{\sigma \beta}\Gamma^\sigma_{\gamma a}-\Gamma^\mu_{\sigma \gamma}\Gamma^\sigma_{\beta a})](http://upload.wikimedia.org/math/a/d/7/ad7e5826a4a4867bc422065f07658a2f.png)
![G_{\mu \nu}~~=[S3] \times {8 \pi G \over c^4} T_{\mu \nu}](http://upload.wikimedia.org/math/5/b/9/5b9a11a28b24aafc4d8bcfde8213e059.png)
![R_{\mu \nu}=[S2]\times [S3] \times {R^a}_{\mu a \nu}](http://upload.wikimedia.org/math/6/7/7/67712c87e2988b00574d6074416b340f.png)





 .
.
![R_{ab[cd;e]} = \, 0](http://upload.wikimedia.org/math/f/4/f/f4fb36895ca1ad0ce1e0a13df3693ec3.png)


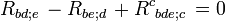




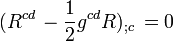

 ,
which is the gravitational potential in joules per kilogram
,
which is the gravitational potential in joules per kilogram![\nabla^2 \Phi [\vec{x},t] = 4 \pi G \rho [\vec{x},t]](http://upload.wikimedia.org/math/8/d/1/8d162e02fb3d4c0a4ece06782e43b860.png)
 is the mass density. The orbit of a
is the mass density. The orbit of a ![\ddot{\vec{x}}[t] = - \nabla \Phi [\vec{x} [t],t] \,.](http://upload.wikimedia.org/math/d/6/a/d6ad46f2e62b895c4ac0e2769fbada1f.png)







 have been divided out. This will reduce to its Newtonian counterpart,
provided
have been divided out. This will reduce to its Newtonian counterpart,
provided





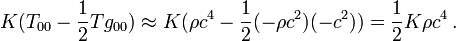


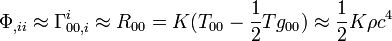



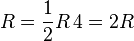
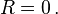


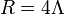




![F_{[\alpha\beta;\gamma]}=\frac{1}{3}\left(F_{\alpha\beta;\gamma} + F_{\beta\gamma;\alpha}+F_{\gamma\alpha;\beta}\right) = 0. \!](http://upload.wikimedia.org/math/9/a/a/9aab3bd95a5046c415cd90da72dea4a7.png)
