Special relativity (SR) (also known as the special theory of relativity or STR) is the physical theory of measurement in inertial frames of reference proposed in 1905 by Albert Einstein (after the considerable and independent contributions of Hendrik Lorentz, Henri Poincaré and others) in the paper "On the Electrodynamics of Moving Bodies". It generalizes Galileo's principle of relativity—that all uniform motion is relative, and that there is no absolute and well-defined state of rest (no privileged reference frames)—from mechanics to all the laws of physics, including both the laws of mechanics and of electrodynamics, whatever they may be. Special relativity incorporates the principle that the speed of light is the same for all inertial observers regardless of the state of motion of the source.
This theory has a wide range of consequences which have been experimentally verified, including counter-intuitive ones such as length contraction, time dilation and relativity of simultaneity, contradicting the classical notion that the duration of the time interval between two events is equal for all observers. (On the other hand, it introduces the space-time interval, which is invariant.) Combined with other laws of physics, the two postulates of special relativity predict the equivalence of matter and energy, as expressed in the mass-energy equivalence formula E = mc2, where c is the speed of light in a vacuum. The predictions of special relativity agree well with Newtonian mechanics in their common realm of applicability, specifically in experiments in which all velocities are small compared with the speed of light. Special relativity reveals that c is not just the velocity of a certain phenomenon—namely the propagation of electromagnetic radiation (light)—but rather a fundamental feature of the way space and time are unified as spacetime. One of the consequences of the theory is that it is impossible for any particle that has rest mass to be accelerated to the speed of light.
The theory is termed "special" because it applies the principle of relativity only to inertial reference frames, i.e. frames of reference in uniform relative motion with respect to each other.Einstein developed general relativity to apply the principle more generally, that is, to any frame so as to handle general coordinate transformations, and that theory includes the effects of gravity. From the theory of general relativity it follows that special relativity will still apply locally (i.e., to first order), and hence to any relativistic situation where gravity is not a significant factor. Inertial frames should be identified with non-rotating Cartesian coordinate systems constructed around any free falling trajectory as a time axis.
- The Principle of Relativity – The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems in uniform translatory motion relative to each other.
- The Principle of Invariant Light Speed – "... light is always propagated in empty space with a definite velocity [speed] c which is independent of the state of motion of the emitting body." (from the preface).That is, light in vacuum propagates with the speed c (a fixed constant, independent of direction) in at least one system of inertial coordinates (the "stationary system"), regardless of the state of motion of the light source.
The derivation of special relativity depends not only on these two explicit postulates, but also on several tacit assumptions (made in almost all theories of physics), including the isotropy and homogeneity of space and the independence of measuring rods and clocks from their past history.
Henri Poincaré provided the mathematical framework for relativity theory by proving that Lorentz transformations are a subset of his Poincaré group of symmetry transformations. Einstein later derived these transformations from his axioms.
Thus many modern treatments of special relativity base it on the single postulate of universal Lorentz covariance, or, equivalently, on the single postulate of Minkowski spacetime.
The constancy of the speed of light was motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous ether but not, contrary to widespread belief, the null result of the Michelson–Morley experiment. However the null result of the Michelson–Morley experiment helped the notion of the constancy of the speed of light gain widespread and rapid acceptance.
Mass-energy equivalence
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy, for E = mc2.
Mass-energy equivalence is a consequence of special relativity. The energy and momentum, which are separate in Newtonian mechanics, form a four-vector in relativity, and this relates the time component (the energy) to the space components (the momentum) in a nontrivial way. For an object at rest, the energy-momentum four-vector is (E, 0, 0, 0): it has a time component which is the energy, and three space components which are zero. By changing frames with a Lorentz transformation in the x direction with a small value of the velocity v, the energy momentum four-vector becomes (E, Ev/c2, 0, 0). The momentum is equal to the energy divided by c2 times the velocity. So the newtonian mass of an object, which is the ratio of the momentum to the velocity for slow velocities, is equal to E/c2.
The principle of relativity, which states that there is no preferred inertial reference frame, dates back to Galileo, and was incorporated into Newtonian Physics. However, in the late 19th century, the existence of electromagnetic waves led physicists to suggest that the universe was filled with a substance known as "aether", which would act as the medium through which these waves, or vibrations travelled. The aether was thought to constitute an absolute reference frame against which speeds could be measured, and could be considered fixed and motionless. Aether supposedly had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, and those waves could interact with matter, yet it offered no resistance to bodies passing through it. The results of various experiments, including the Michelson-Morley experiment, indicated that the Earth was always 'stationary' relative to the aether–something that was difficult to explain, since the Earth is in orbit around the Sun. Einstein's solution was to discard the notion of an aether and an absolute state of rest. Special relativity is formulated so as to not assume that any particular frame of reference is special; rather, in relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in a vacuum is always measured to be c, even when measured by multiple systems that are moving at different (but constant) velocities.
Einstein has said that all of the consequences of special relativity can be derived from examination of the Lorentz transformations.
- Time dilation – the time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames (e.g., the twin paradox which concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that his or her twin sibling has aged much more).
- Relativity of simultaneity – two events happening in two different locations that occur simultaneously in the reference frame of one inertial observer, may occur non-simultaneously in the reference frame of another inertial observer (lack of absolute simultaneity).
- Lorentz contraction – the dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage).
- Composition of velocities – velocities (and speeds) do not simply 'add', for example if a rocket is moving at 2⁄3 the speed of light relative to an observer, and the rocket fires a missile at 2⁄3 of the speed of light relative to the rocket, the missile does not exceed the speed of light relative to the observer. (In this example, the observer would see the missile travel with a speed of 12⁄13 the speed of light.)
- Inertia and momentum – as an object's speed approaches the speed of light from an observer's point of view, its mass appears to increase thereby making it more and more difficult to accelerate it from within the observer's frame of reference.
- Equivalence of mass and energy, E = mc2 – The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that in any reaction a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
Relativity theory depends on "reference frames". The term reference frame as used here is an observational perspective in space at rest, or in uniform motion, from which a position can be measured along 3 spatial axes. In addition, a reference frame has the ability to determine measurements of the time of events using a 'clock' (any reference device with uniform periodicity).
An event is an occurrence that can be assigned a single unique time and location in space relative to a reference frame: it is a "point" in space-time. Since the speed of light is constant in relativity in each and every reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
Let's define the event to have space-time coordinates (t,x,y,z) in system S and (t′,x′,y′,z′) in S′. Then the Lorentz transformation specifies that these coordinates are related in the following way:
is the Lorentz factor and c is the speed of light in a vacuum.
The y and z coordinates are unaffected; only the x and t axes transformed. These Lorentz transformations form a one-parameter group of linear mappings, that parameter being called rapidity.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
where vT denotes the transpose of v, α(v) = 1/γ(v), and P(v) denotes the projection onto the direction of v.
From the first equation of the Lorentz transformation in terms of coordinate differences
it is clear that two events that are simultaneous in frame S (satisfying Δt = 0), are not necessarily simultaneous in another inertial frame S′ (satisfying Δt′ = 0). Only if these events are colocal in frame S (satisfying Δx = 0), will they be simultaneous in another frame S′.
Writing the Lorentz transformation and its inverse in terms of coordinate differences we get
Suppose we have a clock at rest in the unprimed system S. Two consecutive ticks of this clock are then characterized by Δx = 0. If we want to know the relation between the times between these ticks as measured in both systems, we can use the first equation and find:
This shows that the time Δt' between the two ticks as seen in the 'moving' frame S' is larger than the time Δt between these ticks as measured in the rest frame of the clock. This phenomenon is called time dilation. Time dilation explains a number of physical phenomena; for example, the decay rate of muons produced by cosmic rays impinging on the Earth's atmosphere.
Similarly, suppose we have a measuring rod at rest in the unprimed system. In this system, the length of this rod is written as Δx. If we want to find the length of this rod as measured in the 'moving' system S', we must make sure to measure the distances x' to the end points of the rod simultaneously in the primed frame S'. In other words, the measurement is characterized by Δt' = 0, which we can combine with the fourth equation to find the relation between the lengths Δx and Δx':
This shows that the length Δx' of the rod as measured in the 'moving' frame S' is shorter than the length Δx in its own rest frame. This phenomenon is called length contraction or Lorentz contraction.
These effects are not merely appearances; they are explicitly related to our way of measuring time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals will be different in another coordinate system moving with respect to the first, unless the events are also simultaneous. Similarly, these effects also relate to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spatial distance from each other when seen from another moving coordinate system. However, the space-time interval will be the same for all observers. The underlying reality remains the same. Only our perspective changes.
Therefore, if causality is to be preserved, one of the consequences of special relativity is that no information signal or material object can travel faster than light in a vacuum. However, some things can still move faster than light. For example, the location where the beam of a search light hits the bottom of a cloud can move faster than light when the search light is turned rapidly.
Even without considerations of causality, there are other strong reasons why
faster-than-light travel is forbidden by special relativity. For example, if a
constant force is applied to an object for a limitless amount of time, then
integrating F = dp/dt gives a momentum that grows without
bound, but this is simply because 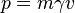 approaches infinity as v
approaches c. To an observer who is not accelerating, it appears as
though the object's inertia is increasing, so as to produce a smaller
acceleration in response to the same force. This behavior is in fact observed in
particle accelerators.
approaches infinity as v
approaches c. To an observer who is not accelerating, it appears as
though the object's inertia is increasing, so as to produce a smaller
acceleration in response to the same force. This behavior is in fact observed in
particle accelerators.
If the observer in S sees an object moving along the x axis at velocity w, then the observer in the S' system, a frame of reference moving at velocity v in the x direction with respect to S, will see the object moving with velocity w' where
This equation can be derived from the space and time transformations above.
Notice that if the object were moving at the speed of light in the
S system (i.e. w = c), then
it would also be moving at the speed of light in the S' system. Also,
if both w and v are small with respect to the speed of
light, we will recover the intuitive Galilean transformation of velocities:  .
.
The usual example given is that of a train (call it system K) travelling due east with a velocity v with respect to the tracks (system K'). A child inside the train throws a baseball due east with a velocity u with respect to the train. In classical physics, an observer at rest on the tracks will measure the velocity of the baseball as v + u.
In special relativity, this is no longer true. Instead, an observer on the
tracks will measure the velocity of the baseball as 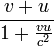 .
If u and v
are small compared to c, then the above
expression approaches the classical sum v +
u.
.
If u and v
are small compared to c, then the above
expression approaches the classical sum v +
u.
In the more general case, the baseball is not necessarily travelling in the
same direction as the train. To obtain the general formula for Einstein velocity
addition, suppose an observer at rest in system K measures the velocity of an object as 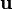 .
Let K' be an inertial system such that the
relative velocity of K to K' is
.
Let K' be an inertial system such that the
relative velocity of K to K' is  ,
where
,
where 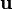 and
and  are now vectors in R3. An observer
at rest in K' will then measure the velocity
of the object as
are now vectors in R3. An observer
at rest in K' will then measure the velocity
of the object as
where  and
and  are the components of
are the components of 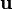 parallel and perpendicular, respectively, to
parallel and perpendicular, respectively, to  ,
and
,
and  .
.
Einstein velocity addition is commutative only when  and
and 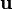 are parallel. In fact,
are parallel. In fact,
,where gyr is the mathematical abstraction of Thomas precession into an operator called Thomas gyration and given by
The gyr operator forms the foundation of gyrovector spaces.
Einstein's addition of colinear velocites is consistent with the Fizeau experiment which determined the speed of light in a fluid moving parallel to the light, but no experiment has ever tested the formula for the general case of non-parallel velocities.
In addition to modifying notions of space and time, special relativity forces one to reconsider the concepts of mass, momentum, and energy, all of which are important constructs in Newtonian mechanics. Special relativity shows, in fact, that these concepts are all different aspects of the same physical quantity in much the same way that it shows space and time to be interrelated.
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses conservation laws. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple thought experiments using the Newtonian definitions of momentum and energy, one sees that these quantities are not conserved in SR. One can rescue the idea of conservation by making some small modifications to the definitions to account for relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
The energy and momentum of an object with invariant mass m (also called rest mass in the case of a single particle), moving with velocity v with respect to a given frame of reference, are given by
respectively, where γ (the Lorentz factor) is given by
The quantity γm is often called the relativistic mass of the object in the given frame of reference, although recently this concept is falling into disuse, and Lev B. Okun suggested that "this terminology [...] has no rational justification today", and should no longer be taught.Other physicists, including Wolfgang Rindler and T. R. Sandin, have argued that relativistic mass is a useful concept and there is little reason to stop using it. See Mass in special relativity for more information on this debate. Some authors use the symbol m to refer to relativistic mass, and the symbol m0 to refer to rest mass.
The energy and momentum of an object with invariant mass m are related by the formulas
The first is referred to as the relativistic energy-momentum equation. While the energy E and the momentum p depend on the frame of reference in which they are measured, the quantity E2 − (pc)2 is invariant, being equal to the squared invariant mass of the object (up to the multiplicative constant c4).
It should be noted that the invariant mass of a system
is greater than the sum of the rest masses of the particles it is composed of (unless they are all stationary with respect to the center of mass of the system, and hence to each other). The sum of rest masses is not even always conserved in closed systems, since rest mass may be converted to particles which individually have no mass, such as photons. Invariant mass, however, is conserved and invariant for all observers, so long as the system remains closed. This is due to the fact that even massless particles contribute invariant mass to systems, as also does the kinetic energy of particles. Thus, even under transformations of rest mass to photons or kinetic energy, the invariant mass of a system which contains these energies still reflects the invariant mass associated with them.
Mass–energy equivalence
For massless particles, m is zero. The relativistic energy-momentum equation still holds, however, and by substituting m with 0, the relation E = pc is obtained; when substituted into Ev = c2p, it gives v = c: massless particles (such as photons) always travel at the speed of light.
Looking at the above formula for invariant mass of a system, one sees that, when a single massive object is at rest (v = 0, p = 0), there is a non-zero mass remaining: mrest = E/c2. The corresponding energy, which is also the total energy when a single particle is at rest, is referred to as "rest energy". In systems of particles which are seen from a moving inertial frame, total energy increases and so does momentum. However, for single particles the rest mass remains constant, and for systems of particles the invariant mass remain constant, because in both cases, the energy and momentum increases subtract from each other, and cancel. Thus, the invariant mass of systems of particles is a calculated constant for all observers, as is the rest mass of single particles.
The mass of systems and conservation of invariant mass
The inertial frame in which the momenta of all particles sums to zero is
called the center of momentum frame. In this
special frame, the relativistic energy-momentum equation has 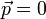 ,
and thus gives the invariant mass of the system as merely the total energy of
all parts of the system, divided by c2
,
and thus gives the invariant mass of the system as merely the total energy of
all parts of the system, divided by c2
An increase in the energy of such a system which is caused by translating the system to an inertial frame which is not the center of momentum frame, causes an increase in energy and momentum without an increase in invariant mass. E = mc2, however, applies only to closed systems in their center-of-momentum frame where momentum sums to zero.
Closed (isolated) systems
In a closed system (i.e., in the sense of a totally isolated system) the total energy, the total momentum, and hence the total invariant mass are conserved. Einstein's formula for change in mass translates to its simplest ΔE = Δmc2 form, however, only in non-closed systems in which energy is allowed to escape (for example, as heat and light), and thus invariant mass is reduced. Einstein's equation shows that such systems must lose mass, in accordance with the above formula, in proportion to the energy they lose to the surroundings. Conversely, if one can measure the differences in mass between a system before it undergoes a reaction which releases heat and light, and the system after the reaction when heat and light have escaped, one can estimate the amount of energy which escapes the system. In both nuclear and chemical reactions, such energy represents the difference in binding energies of electrons in atoms (for chemistry) or between nucleons in nuclei (in atomic reactions). In both cases, the mass difference between reactants and (cooled) products measures the mass of heat and light which will escape the reaction, and thus (using the equation) give the equivalent energy of heat and light which may be emitted if the reaction proceeds.
In chemistry, the mass differences associated with the emitted energy are around one-billionth of the molecular mass. However, in nuclear reactions the energies are so large that they are associated with mass differences, which can be estimated in advance, if the products and reactants have been weighed (atoms can be weighed indirectly by using atomic masses, which are always the same for each nuclide). Thus, Einstein's formula becomes important when one has measured the masses of different atomic nuclei. By looking at the difference in masses, one can predict which nuclei have stored energy that can be released by certain nuclear reactions, providing important information which was useful in the development of nuclear energy and, consequently, the nuclear bomb. Historically, for example, Lise Meitner was able to use the mass differences in nuclei to estimate that there was enough energy available to make nuclear fission a favorable process. The implications of this special form of Einstein's formula have thus made it one of the most famous equations in all of science.
Because the E = mc2 equation applies only to isolated systems in their center of momentum frame, it has been popularly misunderstood to mean that mass may be converted to energy, after which the mass disappears. However, popular explanations of the equation as applied to systems include open systems for which heat and light are allowed to escape, when they otherwise would have contributed to the mass (invariant mass) of the system.
Historically, confusion about mass being "converted" to energy has been aided by confusion between mass and "matter", where matter is defined as fermion particles. In such a definition, electromagnetic radiation and kinetic energy (or heat) are not considered "matter." In some situations, matter may indeed be converted to non-matter forms of energy (see above), but in all these situations, the matter and non-matter forms of energy still retain their original mass.
For closed/isolated systems, mass never disappears in the center of momentum frame, because energy cannot disappear. Instead, this equation, in context, means only that when any energy is added to, or escapes from, a system in the center-of-momentum frame, the system will be measured as having gained or lost mass, in proportion to energy added or removed. Thus, in theory, if an atomic bomb were placed in a box strong enough to hold its blast, and detonated upon a scale, the mass of this closed system would not change, and the scale would not move. Only when a transparent "window" was opened in the super-strong plasma-filled box, and light and heat were allowed to escape in a beam, and the bomb components to cool, would the system lose the mass associated with the energy of the blast. In a 21 kiloton bomb, for example, about a gram of light and heat is created. If this heat and light were allowed to escape, the remains of the bomb would lose a gram of mass, as it cooled. In this thought-experiment, the light and heat carry away the gram of mass, and would therefore deposit this gram of mass in the objects that absorb them.[35]
Force
where p is the momentum as defined above (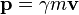 )
and "m" is the invariant
mass. Thus, the force is given by
)
and "m" is the invariant
mass. Thus, the force is given by
Carrying out the derivatives gives
which, taking into account the identity  ,
can also be expressed as
,
can also be expressed as
If the acceleration is separated into the part parallel to the velocity and the part perpendicular to it, one gets
Consequently in some old texts, γ3m is referred to as the longitudinal mass, and γm is referred to as the transverse mass, which is the same as the relativistic mass. See mass in special relativity.
Kinetic energy
If in the initial state the body was at rest (γ0 = 1) and in the final state it has speed v (γ1 = γ), the kinetic energy is K = (γ − 1)mc2, a result that can be directly obtained by subtracting the rest energy mc2 from the total relativistic energy γmc2.
Physics in spacetime
Here, we see how to write the equations of special relativity in a manifestly Lorentz covariant form. The position of an event in spacetime is given by a contravariant four vector whose components are:
where x1 = x and x2 = y and x3 = z as usual. We define x0 = ct so that the time coordinate has the same dimension of distance as the other spatial dimensions; in accordance with the general principle that space and time are treated equally, so far as possible. Superscripts are contravariant indices in this section rather than exponents except when they indicate a square. Subscripts are covariant indices which also range from zero to three as with the spacetime gradient of a field φ:
Metric and transformations of coordinates
Having recognised the four-dimensional nature of spacetime, we are driven to employ the Minkowski metric, η, given in components (valid in any inertial reference frame) as:
which is equal to its reciprocal, ηαβ, in those frames.
Then we recognize that coordinate transformations between inertial reference frames are given by the Lorentz transformation tensor Λ. For the special case of motion along the x-axis, we have:
where there is an implied summation of  and
and  from 0 to 3 on the right-hand side in accordance with the Einstein summation
convention. The Poincaré group is the most general group of
transformations which preserves the Minkowski metric and
this is the physical symmetry underlying special relativity.
from 0 to 3 on the right-hand side in accordance with the Einstein summation
convention. The Poincaré group is the most general group of
transformations which preserves the Minkowski metric and
this is the physical symmetry underlying special relativity.
All proper physical quantities are given by tensors. So to transform from one frame to another, we use the well-known tensor transformation law
Where  is the reciprocal matrix of
is the reciprocal matrix of 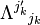 .
.
which is the Lorentz transformation given above. All tensors transform by the same rule.
The squared length of the differential of the position four-vector  constructed using
constructed using
is an invariant. Being invariant means that it takes the same value in all
inertial frames, because it is a scalar (0 rank tensor), and so no Λ appears in
its trivial transformation. Notice that when the line element  is negative that
is negative that  is the differential of proper
time, while when
is the differential of proper
time, while when  is positive,
is positive, 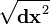 is differential of the proper distance.
is differential of the proper distance.
Velocity and acceleration in 4D
Recognising other physical quantities as tensors also simplifies their transformation laws. First note that the velocity four-vector Uμ is given by
Recognising this, we can turn the awkward looking law about composition of velocities into a simple statement about transforming the velocity four-vector of one particle from one frame to another. Uμ also has an invariant form:
So all velocity four-vectors have a magnitude of c. This is an
expression of the fact that there is no such thing as being at coordinate rest
in relativity: at the least, you are always moving forward through time. The acceleration 4-vector
is given by  .
Given this, differentiating the above equation by τ produces
.
Given this, differentiating the above equation by τ produces
So in relativity, the acceleration four-vector and the velocity four-vector are orthogonal.
Momentum in 4D
The momentum and energy combine into a covariant 4-vector:
where m is the invariant mass.
The invariant magnitude of the momentum 4-vector is:
The rest energy is related to the mass according to the celebrated equation discussed above:
Force in 4D
To use Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the four-force. It is the rate of change of the above energy momentum four-vector with respect to proper time. The covariant version of the four-force is:
In the rest frame of the object, the time component of the four force is zero
unless the "invariant
mass" of the object is changing (this requires a non-closed system in which
energy/mass is being directly added or removed from the object) in which case it
is the negative of that rate of change of mass, times c. In general,
though, the components of the four force are not equal to the components of the
three-force, because the three force is defined by the rate of change of
momentum with respect to coordinate time, i.e.  while the four force is defined by the rate of change of momentum with respect
to proper time, i.e.
while the four force is defined by the rate of change of momentum with respect
to proper time, i.e.  .
.
Relativity and unifying electromagnetism
Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation-speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic field. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Electromagnetism in 4D
Maxwell's equations in the 3D form are already consistent with the physical content of special relativity. But we must rewrite them to make them manifestly invariant.
The charge density
 and current density
and current density
![[J_x,J_y,J_z] \!](http://upload.wikimedia.org/math/b/b/d/bbda214f893097e844ca77ead238f3ea.png) are unified into the current-charge 4-vector:
are unified into the current-charge 4-vector:
The law of charge conservation,  ,
becomes:
,
becomes:
The electric field
![[E_x,E_y,E_z] \!](http://upload.wikimedia.org/math/d/3/2/d32f98f806351056af76cc06b92c6675.png) and the magnetic
induction
and the magnetic
induction ![[B_x,B_y,B_z] \!](http://upload.wikimedia.org/math/4/b/0/4b079b6a4f51cb469344ef7055ab9ad5.png) are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
The density, 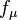 ,
of the Lorentz force,
,
of the Lorentz force,
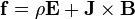 ,
exerted on matter by the electromagnetic field becomes:
,
exerted on matter by the electromagnetic field becomes:
Faraday's law of induction, 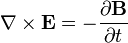 ,
and Gauss's law for magnetism,
,
and Gauss's law for magnetism, 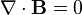 ,
combine to form:
,
combine to form:
The electric displacement ![[D_x,D_y,D_z] \!](http://upload.wikimedia.org/math/c/3/e/c3e5dbe4aa735fb8c654c990852fdadf.png) and the magnetic field
and the magnetic field
![[H_x,H_y,H_z] \!](http://upload.wikimedia.org/math/e/4/a/e4a5c51917445501b7ac0e606c9bba14.png) are now unified into the (rank 2 antisymmetric contravariant) electromagnetic
displacement tensor:
are now unified into the (rank 2 antisymmetric contravariant) electromagnetic
displacement tensor:
Ampère's law,  ,
and Gauss's law,
,
and Gauss's law, 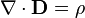 ,
combine to form:
,
combine to form:
In a vacuum, the constitutive equations are:
the constitutive equations may, in a vacuum, be combined with Ampère's law etc. to get:
The energy density of the electromagnetic field combines with Poynting vector and the Maxwell stress tensor to form the 4D electromagnetic stress-energy tensor. It is the flux (density) of the momentum 4-vector and as a rank 2 mixed tensor it is:
where 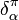 is the Kronecker
delta. When upper index is lowered with η, it becomes symmetric and is part
of the source of the gravitational field.
is the Kronecker
delta. When upper index is lowered with η, it becomes symmetric and is part
of the source of the gravitational field.
The conservation of linear momentum and energy by the electromagnetic field is expressed by:
where 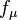 is again the density of the Lorentz force. This equation can be deduced from
the equations above (with considerable effort).
is again the density of the Lorentz force. This equation can be deduced from
the equations above (with considerable effort).
Special relativity is accurate only when the absolute value of the gravitational potential is much less than c2. In a strong gravitational field, one must use general relativity. General relativity becomes special relativity at the limit of weak field. At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravity. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10−20) and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.
Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) — thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See Status of special relativity for a more detailed discussion.
- The Trouton–Noble experiment showed that the torque on a capacitor is independent of position and inertial reference frame.
- The famous Michelson-Morley experiment gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
- The Fizeau experiment measured the speed of light in moving media, with results that are consistent with relativistic addition of colinear velocities.
![]() Copyright(c) 2007
- 2012. All rights reserved.
Copyright(c) 2007
- 2012. All rights reserved.

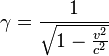



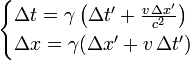
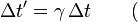 for events satisfying
for events satisfying 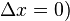
 for events satisfying
for events satisfying 
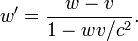


,](http://upload.wikimedia.org/math/c/a/f/caf0508d64d8dc8e697598545fe5c209.png)
![gyr[\mathbf{u},\mathbf{v}]\mathbf{w}=\ominus(\mathbf{u} \oplus \mathbf{v}) \oplus (\mathbf{u} \oplus (\mathbf{v} \oplus \mathbf{w}))](http://upload.wikimedia.org/math/a/b/8/ab8678f13179c069c9f0f1a764c6f9fe.png)




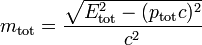
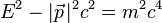

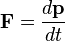










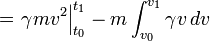





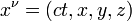





![T^{\left[i_1',i_2',\dots,i_p'\right]}_{\left[j_1',j_2',\dots,j_q'\right]} =
\Lambda^{i_1'}{}_{i_1}\Lambda^{i_2'}{}_{i_2}\cdots\Lambda^{i_p'}{}_{i_p}
\Lambda_{j_1'}{}^{j_1}\Lambda_{j_2'}{}^{j_2}\cdots\Lambda_{j_q'}{}^{j_q}
T^{\left[i_1,i_2,\dots,i_p\right]}_{\left[j_1,j_2,\dots,j_q\right]}](http://upload.wikimedia.org/math/5/f/1/5f10063892eef437b2a03d2a0fa9d05d.png)


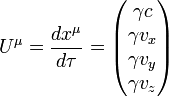
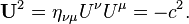






 is the proper time.
is the proper time.


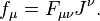
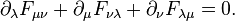



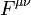 by
by


